El parque de Magdalena del Mar es un astroide

Crónica de hace un año

6:00 pm

Fuimos un rato al parque Túpac Amaru (ese que está en Magdalena del Mar), donde había una feria.

6:10 pm

Propuse dar unas vueltas a hablar de lo que sea por el parque. Al andar, algo raro me llamó la atención: las veredas parecían seguir la forma de una ecuación paramétrica.

6:20 pm

De repente, recordé el nombre de la ecuación: el astroide. Mientras caminaba sobre el lugar geométrico, pensé que podría encajar la figura dentro de un conjunto más grande de curvas planas.

6:30 pm

¿De dónde surge un astroide?

Pensé en la estela que deja un punto $P$ de un círculo que rueda a lo largo de una línea fija $L$ (la directriz). El nombre técnico es trocoide. Es una de las curvas ampliamente usadas para el diseño de engranajes.

Aquí, de inmediato, me surgieron las clasificaciones:

• Si el punto $P$ está en la circunferencia será llamada cicloide normal o cicloide común.
• Si el punto $P$ está dentro del círculo, se llamará trocoide curtate (contraída).
• Si el punto $P$ está fuera del círculo, se llamará trocoide prolate (extendida).

Bastan tres condiciones para establecer un nombre más preciso.

Sigamos. Si el radio del círculo es $r$, y pensamos en $P$ como la distancia del centro hacia el punto fijo, entonces tendremos las ecuaciones paramétricas:

$$ x(\varphi) = r \varphi - P \sin \varphi $$ $$ y(\varphi) = r - P \cos \varphi $$ En nuestro caso, $r = P$.

¿Qué curioso que un punto cambie tantas cosas? Así de lindas son las matemáticas.

6:40 pm

Mi mente, siempre inquieta, me llevó a una nueva reflexión:

Si rodamos sobre una línea $L$, ¿por qué no rodar sobre cualquier otra figura, sobre cualquier otra curva plana? ¿Qué pasaría si no nos limitáramos a la simpleza de la recta? Después de todo, las matemáticas no tienen límites.

Una idea bastante natural es pensar que, en lugar de hacer rodar un círculo sobre una línea, ahora tenemos un círculo rodante que gira sobre otro círculo base estacionario. La estela de este giro producirá una nueva curva.

Una vez más, se abre una clasificación, pero esta vez, pensando en si el círculo generatriz rueda por fuera o por dentro del círculo base inmóvil.

• Si rueda por fuera, le llamaremos epicicloide.
• Si rueda por dentro, le pondremos de nombre hipocicloide.

6:55 pm

Otra vez me siento incómodo con una clasificación incompleta. El simple hecho de que existan epicicloide e hipocicloide me hace regresar a la clasificación de rodar sobre la línea. ¿Y si $P$ es mayor o menor al radio $r$ de este círculo rodante? Sí, efectivamente, también hay más opciones:

• Epitrocoide (círculo generatriz fuera del círculo estacionario)
  • Epicicloide contraída ($P$ dentro del generador)
  • Epicicloide extendida ($P$ fuera del generador)
• Hipotrocoide (círculo generatriz dentro del círculo estacionario)
  • Hipocicloide contraída ($P$ dentro del generador)
  • Hipocicloide extendida ($P$ fuera del generador)

Y hay una posibilidad más, algo más exótica: la pericicloide, donde la que rueda ahora es estacionaria (los radios cambian papeles), pero esa la dejaremos de lado por ahora.

7:10 pm

Ya estamos listos para el astroide con sus ecuaciones. Desde un punto de vista puramente intuitivo, un astroide se ve como una estrella inflada de 4 puntas. El término más apropiado para las puntas, en este contexto, sería el de cúspides.

Así que armemos un astroide simple, con cúspides de longitud $1$ respecto al origen.

$$ x(\varphi) = \sin ^3 (\varphi) $$ $$ y(\varphi) = \cos ^3 (\varphi), $$

donde $0 \leq \varphi \leq 2\pi.$

10:00 pm

Ya en casa, vamos a echar mano de Geogebra para graficar el astroide del parque con las ecuaciones paramétricas de más arriba.

Lo único que agregaremos para darle un toque de dinamismo es un control deslizante. Lo llamaremos $\varphi$, para que la figura se mueva mientras exploramos la curva.

Te juego el codiguillo:

varphi = 2 pi
Curva(sen³(u), cos³(u), u, 0, varphi)

Agregamos algo de color y listo, ahí está nuestro astroide. Con el control deslizante $\varphi$ en acción, la figura cobra vida, mostrando su ritmo.

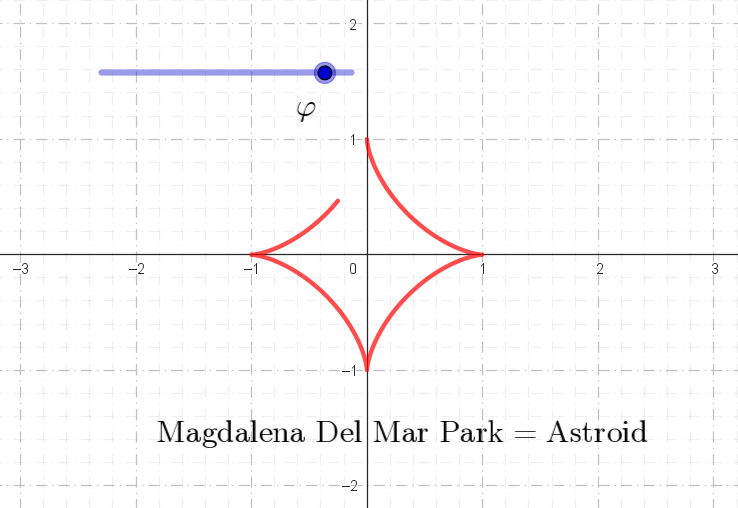
Ahora, al compararla con la foto panorámica del parque de Magdalena del Mar, la conexión entre la geometría y el paisaje se vuelve interesante. Tenemos un juego entre lo físico y lo abstracto.

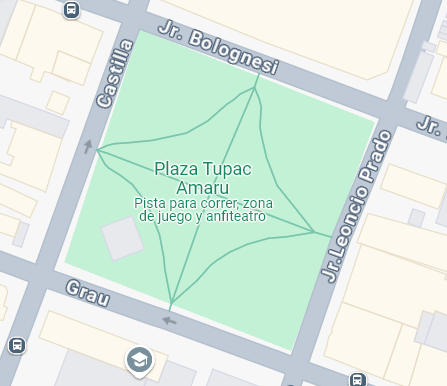
Coincidencia

Es rarísimo topar con algo así, salir a divertirte y terminar haciendo hora con algo de geometría de curvas planas. Pero, claro, nunca sabes cuándo la matemática va a decidir aparecer… ¡y a veces lo hace justo mientras haces hora en una feria!